В статье рассматриваются проблемы анализа результатов Единого государственного экзамена на федеральном и региональном уровнях, некоторые социальные аспекты его проведения, роль ЕГЭ в системе повышения качества общеобразовательной подготовки школьников, выявляется ряд инструментальных недостатков ЕГЭ, влияющих на его итоги.
С 2005 года в открытом доступе стали появляться официальные общероссийские итоги Единого государственного экзамена. Их автором является Федеральный институт педагогических измерений (ФИПИ), осуществляющий содержательное и аналитическое сопровождение ЕГЭ. Помимо издания сборников ФИПИ свои исследования также выставляет на сайт (см. www.fipi.ru). К настоящему времени на сайте ФИПИ имеются годовые отчеты о проведении экзамена с 2005 по 2008 годы почти по всем дисциплинам. Несмотря на то, что отчеты ФИПИ носят название «аналитические», большей частью они посвящены констатации фактов и не объясняют причин тех или иных результатов ЕГЭ. К сожалению, они также оказались политизированы полемикой о целесообразности ЕГЭ и не много сообщают о его действительных проблемах. При этом вольно или невольно искажается истинная картина проведения экзамена (в нашем случае мы говорим только о предмете «математика»). Назначение отчетов ФИПИ можно скорее отнести к обоснованию полезности проведения таких испытаний. Поэтому в целях определения проблем, связанных с проведением ЕГЭ, нами был предпринят параллельный его анализ.
Авторы не ставили задачу рассмотреть итоги ЕГЭ по всем дисциплинам. Для этого мы просто не располагаем исходной информацией. В нашем распоряжении имеется лишь некоторая статистика ЕГЭ по математике в Омской области в 2005—08 годах, т.е. за период, когда экзамен по этой дисциплине был в регионе обязательным для всех учащихся. Опираясь на материалы, опубликованные ФИПИ, и статистику итогов экзамена по математике в Омской области рассмотрим следующие вопросы:
— насколько возможен анализ результатов ЕГЭ и как с этой задачей справляется ФИПИ и региональные органы управления образованием, например, в лице Министерства образования Омской области;
— какие проблемы необходимо решить для того, чтобы подведение итогов экзамена способствовало повышению общеобразовательной подготовки школьников.
Обработать результаты ЕГЭ в целом по стране могут те инстанции, которые располагают для этого соответствующими данными — организаторы проведения экзамена и разработчики контрольно-измерительных материалов (КИМов): Министерство образования и науки РФ, Федеральный центр тестирования (ФЦТ) и Федеральный институт педагогических измерений. Несмотря на то, что экзамен проводится с 2001 года, отчеты по их итогам обнародованы только за последние четыре года. Что же можно узнать из них о результатах ЕГЭ по математике?
Прежде всего, составители официальных итогов ЕГЭ сразу оговариваются, что их работа не претендует на полноту и всесторонность представления результатов «из-за невозможности отражения выполнения всех вариантов КИМов и временных ограничений». Причем эта оговорка кочует в отчетах из года в год [1, с.5]; [2, с.6]; [3, с.6]. Однако ФИПИ лукавит, ссылаясь на трудности работы с большим количеством КИМов и ограниченность сил. Проблемы анализа ЕГЭ связаны не с многочисленностью вариантов, нехваткой сотрудников или отсутствием времени, а с самим экзаменом, с действующей структурой сбора, накопления и представления информации о его результатах.
Обратим внимание на характер сведений, с которыми имеют дело аналитики экзамена. Результатом ЕГЭ по математике считается факт отметки школьником одной из четырех альтернатив ответа на задания в части «А» (крестик в бланке), краткий ответ в части «В» (число) и баллы за решение части «С» (балл). Также бланк регистрации помимо фамилии и паспортных данных фиксирует индивидуальный номер участника, регион, муниципальное образование, образовательное учреждение, класс, пункт проведения ЕГЭ, номер аудитории, дата проведения экзамена, предмет, вариант. Региональные центры обработки информации (РЦОИ) в дополнение к итогам выполнения работ направляют в Федеральный центр тестирования (ФЦТ) информацию об образовательных учреждениях, указывая кроме прочего (наименование, юридический адрес, данные об аттестации и аккредитации и т.д.) их местонахождение, тип, вид и форму собственности.
В 2005 году ФЦТ обработал результаты ЕГЭ по математике на 680 тыс. чел. (52% от общего числа выпускников школ) [1, с.8], в 2006 г. — 623 тыс. (47,7%) [2, с.10], в 2007 г. — 605 тыс. (52,9%) [3, с.10], в 2008г. — 938 тыс. (88,2%) [4, с.10].
Вопрос: что можно получить в результате обработки и анализа таких данных?
Ответ: ничего или почти ничего. Поясним почему.
Итоги ЕГЭ в виде усредненной оценки по стране или территориям (тестовый балл или процент учащихся, получивших те или иные аттестационные отметки) мало что говорит о состоянии и проблемах математической подготовки школьников. Для глубокого анализа результатов ЕГЭ необходимо выделить группы школьников, описать их результат и объяснить его причины. Однако перечень признаков для группировки выпускников школ, заложенных структурой сведений об участниках очень незначителен: пол участника, тип и вид школы, местность ее нахождения, форма собственности – и все! Не случайно аналитики ФИПИ, не имея возможности провести иной группировки, ежегодно повторяют более чем банальные выводы: городские школьники задания выполняют лучше сельских, выпускники обычных школ – лучше вечерних, учащиеся гимназий, лицеев и школ с углубленным изучением предметов – лучше школ обычных, в крупных населенных пунктах – лучше чем, в малых (см. [1, с.14]; [2, с. 17, 41—42]; [3, с.19—20]), [4, с.48]. Такие заключения можно сделать, не прибегая к ЕГЭ.
Выход своим аналитическим усилиям ФИПИ находит в выделении групп учащихся по степени успешности выполнения экзаменационной работы: двоечников, троечников, хорошистов и отличников, а затем рассматривает их результаты по типам задач. Однако на уровне федерального центра это занятие в значительной мере лишено смысла. О чем, например, свидетельствуют данные, что логарифмические неравенства решили в стране 66,8% школьников [3, с.52]? Это средняя температура даже не по больнице, а по стране. Успешность решения различных типов задач имеет смысл рассматривать на уровне класса, максимум – школы. ФИПИ, изучая затруднения учащихся, фактически выполняет работу, которая должна быть проведена по итогам экзамена в каждом общеобразовательном учреждении. Анализ, который ФИПИ представляет в своих отчетах, более необходим разработчикам образовательных стандартов и КИМов, но не педагогам, для которых гораздо важнее знание конкретных затруднений именно своих, а не среднестатистических выпускников.
Сложность изучения результатов ЕГЭ по математике заключается, кроме того, в отсутствии информации о реальных трудностях учащихся. Требования технологичности обработки результатов заставляет записывать ответы числом или предлагать альтернативы для выбора. Но главное, за результатом не видно логики рассуждения экзаменуемых. В этих условиях умозаключения специалистов ФИПИ о проблемах школьников строятся на догадках, основанных больше на практике непосредственного общения с учащимися, чем на результатах выполнения работ. Даже анализ итогов части «С» возможен лишь постольку, поскольку специалистам ФИПИ удается, что называется «вживую», поработать с ответами выпускников и самими учащимися, либо с обобщенными аналитическими справками, подготовленными региональными экспертами. Так, например, проблема решения алгебраического задания С5 в 2006 году, связанная с тем, что в его условии не имелось никаких ориентиров, облегчающих нахождение способа решения, выявилась для авторов КИМов только в беседах со школьниками, участвовавшими в пробных и репетиционных ЕГЭ [2, с.55].
Не удивительно, что, обладая столь колоссальным (более полумиллиона работ только по математике), сколько и пустым (в виде крестиков и готовых ответов) массивом информации, ФИПИ вынужден гадать о действительных затруднениях выпускников, что хорошо видно из содержания отчетов. Показательным в этом отношении являются оговорки, которыми изобилует анализ ФИПИ типа: «ВИДИМО», «ПО-ВИДИМОМУ», «ВОЗМОЖНО», «ВЕРОЯТНО», «МОЖЕТ БЫТЬ». Чтобы не быть голословными процитируем, например, некоторые фрагменты отчета ФИПИ 2006 года (выделено нами):
«Поскольку сразу в условие задачи не удается подставить значение переменной, а предварительно необходимо преобразовать данные задачи (представить логарифм произведения в виде суммы логарифмов), то видимо именно этот шаг вызывает наибольшее затруднение» [2. с.44].
«Немного более низкие результаты выполнения заданий типа №1 и №2, по-видимому, связаны с тем, что после применения свойств радикалов от учеников требовалось вычислить значение корня, что способствовало появлению вычислительных ошибок» [2, с.46].
«Некоторое снижение результатов, по-видимому, объясняется тем, что после умножения степеней (34а x 3 – 2а = 32а) выпускники должны вычислить значение выражения…» [2, с.47].
«…менее подготовленные учащиеся лучше выполняют преобразование суммы логарифмов в логарифм произведения, чем разность логарифмов в логарифм частного. Видимо, именно это повлияло на снижение результатов при решении логарифмического уравнения [2, с.49].
«Возможно, что трудности с решением этого уравнения у слабо подготовленных школьников связаны с несколько необычным видом уравнения…» [2, с.50].
«Вероятнее всего, более высокий результат при решении этого типа уравнения объясняется формой представления условия задания…» [2, с.51].
«Возможно, что некоторое снижение результатов связано с тем, что при нахождении области определения уравнения типа №3 нужно было учитывать два фактора…» [2, с.52].
«Трудность этого задания, возможно, состояла в том, что от учащихся требовалось самостоятельно по графикам определить абсциссы точек пересечения двух графиков» [2, с.54].
«С заданием типа №1 справляются несколько хуже: дают верный ответ в среднем 22,4% выпускников, среди них только 66,1%, получивших отметку “5”. Возможно, это связано с двумя обстоятельствами. Во-первых, в этом задании более длинная цепочка вычислений (4 слагаемых вместо 3 или 2), что, очевидно, с большей вероятностью может приводить к арифметическим ошибкам. Во-вторых, более низкий результат мог быть обусловлен тем, что учащиеся меньше ошибок допускают, применяя определение четной функции (f(– x) = f(x)), чем нечетной (f(– x) = – f(x)). А в задании №1 использовалось определение именно нечетной функции» [2, с.60].
Не спасают положение и дистракторы — варианты ответов, полученные с использованием типичных ошибочных действий школьников, по той простой причине, что заполнение бланков заданий в условиях гарантированной тройки у значительной их части происходит методом элементарного гадания. Так, например, выпускники одной из вечерних школ Омской области выполнили свою работу на экзамене за 15 минут, заполнив адресную часть бланка и понаставив крестов в бланке №1. Анализ дистракторов в этом случае добросовестных исследователей просто приведет к заблуждениям.
Другая проблема: сопоставление итогов ЕГЭ по годам. О том, как выявляются тенденции в качестве подготовки школьников, можно узнать из отчетов ФИПИ. Для этого, по словам авторов, производится шкалирование результатов текущего и предшествующего года на основе единого банка откалиброванных тестовых заданий [1, с.5]. Однако при определении тенденций сравниваются не фактические результаты – количество решенных заданий, а производные от этой оценки – тестовые баллы и аттестационные отметки. В Омской области, например, в 2007 году средний первичный балл (число решенных заданий) и средний процент выполнения работы составили 10,2 и 27,7%, против 9,2 и 24,4% в 2006 году, однако среднеобластной тестовый балл практически не изменился. Число задач, решенных омскими школьниками, увеличилось, а качество математической подготовки почти не улучшилось [7, с.8]. В то же время согласно ФИПИ КИМы не менялись: «По сравнению с 2006 годом в контрольно-измерительных материалах 2007 года не произошло существенных изменений ни по структуре, ни по содержанию» [3, с.12]. О том, почему были повышены нормы выставления положительной аттестационной отметки «3» в 2007 году, мы скажем далее.
К сожалению, недостатки работы ФИПИ обнаруживаются не только при разборе содержания школьных работ, но при анализе общей ситуации организации и проведения ЕГЭ в стране. Материалы ФИПИ в силу дискуссионности вопроса замалчивают несовершенство и проблемы экзамена и тенденциозно освещают его итоги. Отсутствие объективности проявляется в манипулировании цифрами, сокрытии важных обстоятельств проведения ЕГЭ, предвзятости выводов, что становится возможным по причине монополии ФИПИ на информацию. Приведем несколько примеров.
Когда в 2006 году отмечается рост числа участников экзамена из крупных городов, ФИПИ делает вывод о повышении общественного доверия к ЕГЭ [2, с. 16]. Данный вывод сделан без учета обстоятельств расширения перечня экзаменов в регионах-участниках. Что касается математики, то в 2006 году число участников ЕГЭ по предмету в 59 регионах из 69 участвовавших снизилось более чем на 100 тыс. чел. Это следует из статистических таблиц, приводимых самим ФИПИ [1, с.6—8], [2, с.7—10]. Частично произошло это из-за снижения общей численности выпускников школ. Смягчило картину снижения числа участников ЕГЭ в 2006 году присоединение к экзамену новых субъектов федерации (города Москвы, Усть-Ордынского Бурятского АО, Курской и Владимирской областей) и введение его обязательности в Иркутской области (сравнение произведено по данным [1, с.6—9] и [2, с.7—10], численность выпускников школ в 2005 году взята из [5, с.261—279]). В 2006 году в регионах, где число участников ЕГЭ составляет менее 60% выпуска (т.е. где выбор экзамена предположительно добровольный[1]), доля школьников, желающих участвовать в ЕГЭ, снизилась. Например, в Волгоградской области в 2005 году в экзамене по математике приняли участие 48% выпускников, в 2006г. — 33%, Воронежской — 45% и 37%, Астраханской — 53% и 33%, Калужской — 52% и 18%, Тульской — 45% и 35%, Дагестане — 9% и 5%, Северной Осетии — 17% и 13%, Калмыкии — 57% и 52%, Ямало-Ненецком АО — 35% и 33% и т.д.
Среди регионов, где в 2006 году отмечается рост числа участников на добровольной основе можно назвать Камчатскую область (число участников увеличилось на 4 чел. или 0,3%), Чукотский АО (на 71 чел. — 50%), Московская область (на 252 чел. — 24%), Тыва (на 395 чел. — 95%), Башкирия (на 1093 чел. — 10%), Новосибирская область (на 1260 чел. — 25%), Бурятия (на 1352 чел — 15%), Свердловская область (на 9341 чел. или в 32 раза), Татарстан (на 13705 чел. — в 3 раза). Вероятно, зафиксированное ФИПИ увеличение числа участников из крупных городов, дали Екатеринбург и Казань (например, в 2005 году в Свердловской области участвовало 292, в 2006г. — 9633 чел., в Татарстане — 6873 и 20578 чел.) за счет введения обязательности экзамена. На основании этих данных выводы о повышении общественного доверия к ЕГЭ делать, наверное, преждевременно.
В 2006 году ФИПИ приходит к заключению о повышении уровня математической подготовки в целом по стране по сравнению с 2005 годом [2, с.41]. При этом он игнорирует факт изменения состава участников экзамена, а именно, увеличение числа школьников из крупных городов, о котором сам сообщает ранее [2, с.16], где по признанию ФИПИ математическая подготовка выше. Привести данные в сопоставимый вид, указав, как изменились результаты у горожан и сельчан, и дать их анализ отдельно ФИПИ затруднился.
Охват школьников испытаниями ЕГЭ, достаточный для корректного сопоставления качества подготовки выпускников по регионам, меняется ФИПИ на ходу. В 2005—06 годах он должен быть выше 90% выпускников [1, с.8]; [2, с.11], в 2007 году составляет – 80% [3, с.19]. Создается впечатление, что ФИПИ до сих пор не выработал обоснованных критериев для сопоставления результатов экзамена по территориям.
Для отчетов ФИПИ характерно вольное обращение со статистикой. Например, сведения о численности выпускников школ в таблицах за 2006, 2007, 2008 годы не соответствуют действительности [2, с. 7—10], [3, с. 8—10], [4, с. 8—10]. Для подсчета процента участия школьников используются данные о выпускниках школ предыдущего, а не текущего года. В то время как результаты ЕГЭ анализируются, видимо, уже в августе—октябре, информация о выпускниках текущего года из субъектов Российской Федерации поступает в Министерство образования и науки РФ и Росстат («Сведения о дневных общеобразовательных учреждениях» по форме 76-рик) только в середине ноября. В условиях отсутствия свежих данных специалисты института не придумали ничего лучшего, как определять процент участия по выпуску прошлых лет. Это приводит ФИПИ к довольно большим ошибкам. Например, из отчета института мы узнаем, что в 2008 году доля школьников Омской области, участвовавших в ЕГЭ по математике, составила 69% (хотя фактически за счет выпускников прошлых лет этот показатель составил 102%). В результате в 2008 году ФИПИ относит Омскую область к регионам с необязательной формой участия в ЕГЭ [4, с. 7, 43].
Указывая, что значительную часть участников ЕГЭ составляют выходцы из сельской местности, ФИПИ делает вывод о том, что ЕГЭ оправдывает свою роль социального лифта для учащихся отдаленных районов страны [1, с.13—14]. Однако такое заключение следовало бы подкрепить фактом увеличения доли сельских школьников от регионов, где экзамен проводился на добровольной основе. Этого сделано не было. Между тем руководство образования Омской области, например, где процент сельского населения выше среднероссийского, приняло решение об участии в ЕГЭ по математике не из соображений расширения образовательных возможностей сельских учащихся, а по более прозаическим причинам. Министерство образования и науки РФ бесплатно для регионов (т.е. за счет федерального бюджета) создавало инфраструктуру экзамена (вычислительная и множительная техника, оборудование, программное обеспечение и т.д.) в тех из них, где принято решение добровольно участвовать в эксперименте. При этом региональным руководителям образования делался намек, что в последующем оборудование для проведения экзамена придется приобретать самостоятельно. Чтобы сэкономить областной бюджет, было принято соответствующее решение. Понятно, что желания выпускников сельских школ при этом никто не спрашивал.
По признанию самого ФИПИ уровень математической подготовки сельских школьников ниже, чем в городе. Так за что же они так любят ЕГЭ? Причина относительной «популярности» ЕГЭ среди сельских учащихся – это гарантированная тройка в аттестате об образовании даже при заполнении бланков ответов наугад.
На сайте ФИПИ в 2007 году приводится график плотности распределения учащихся в целом по стране, набравших соответствующий балл по различным предметам. По математике этот график выглядит следующим образом (рис.1).
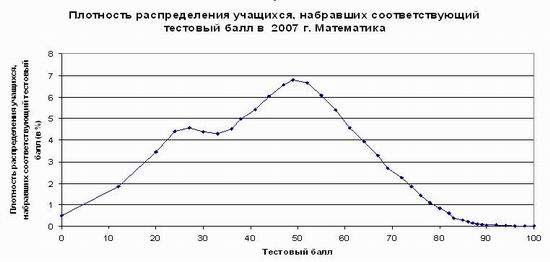
Рис.1. График, опубликованный на сайте ФИПИ по результатам 2007 года
|
Перед нами нормальное распределение, имеющее моду в 49 и выброс значений, соответствующий 27 баллам. ФИПИ не объясняет появление этого выброса (либо потому что не знает, либо не хочет акцентировать внимание на неприглядную для экзамена причину). Между тем это учащиеся, получившие отметку «2», и выполнявшие задания путем гадания ответов. В целом по стране доля школьников, «участвующих» в ЕГЭ по математике с результативностью гадания составляет до 20%. Это отражает действительное отношение учащихся к единому экзамену.
Для доказательства проведем небольшое исследование. Воспользуемся статистикой ЕГЭ по Омской области в 2005году. Обратим внимание, что результаты по Омской области ЕГЭ 2004—2006 и 2007 годов несходны (о причинах мы скажем позже), однако, судя по региональной статистике, выброс значений в 27 тестовых баллов на протяжении всего времени проведения экзамена присутствовал, причем в существенно больших размерах, чем это зафиксировано в 2007 году (рис.2).
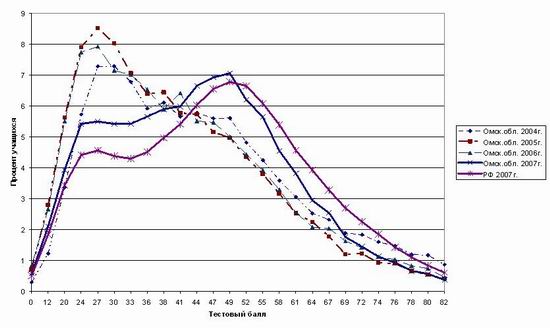
Рис. 2. Распределение учащихся по набранному тестовому баллу по математике
|
Напомним, что задания части «А», где необходимо выбрать ответ, содержат только 4 альтернативы выбора. В случае незнания правильного ответа, средняя вероятность угадывания каждого задания составляет 25%. Посмотрим, какой балл можно получить за решение части «А», используя исключительно угадывание альтернатив ответа. Воспользуемся схемой Бернулли, которая рассматривает вероятность получения искомых результатов в серии независимых испытаний. В нашем случае мы имеем серию из 10 заданий с 4 альтернативами выбора. Угадывание правильного ответа наступает с вероятностью 0,25, ошибка — с вероятностью 0,75. В соответствии с формулой Бернулли
Рn(k) = Ckn pk qn-k, k=0,1,…n
определяем вероятность получения определенного количества баллов путем угадывания в серии из 10 задач, при начислении 1 балла за 1 верный ответ (см. табл. 1).
Таблица 1.
Вероятность получения определенного числа баллов при угадывании и фактический процент двоечников Омской области, получивших баллы за решение части «А»
Число баллов |
Процент вероятности получения результата при угадывании (рассчитано по формуле Бернулли) |
Процент учащихся, не решавших часть «В» и получивших баллы за решение заданий части «А» |
Процент учащихся, не решавших часть «В» и получивших баллы за решение 8 заданий части «А» (без задач А2 и А3) |
| 0 баллов |
5,63135 |
2,497199 |
6,49912 |
| 1 балл |
18,77117 |
9,300464 |
18,92108 |
| 2 балла |
28,15676 |
17,14423 |
25,54826 |
| 3 балла |
25,02823 |
21,37026 |
22,05859 |
| 4 балла |
14,59980 |
18,79302 |
14,42292 |
| 5 баллов |
5,83992 |
13,86265 |
7,619657 |
| 6 баллов |
1,62220 |
8,388026 |
3,52169 |
| 7 баллов |
0,30899 |
4,962382 |
1,120538 |
| 8 баллов |
0,03862 |
2,577237 |
0,288138 |
| 9 баллов |
0,00286 |
0,864415 |
0 |
| 10 баллов |
0,00010 |
0,240115 |
0 |
В части «В» в 2005 году под кодами В1, В2, В3 содержались задания, которые так же как часть «А» относятся к базовому уровню сложности и отличаются только формой записи ответа, исключающей элемент угадывания. Это позволяет выделить учащихся, выполнявших работу преимущественно наугад: т.е. не решивших ни одного из заданий, предполагающих запись краткого ответа.
В таблице 1 приведено распределение по баллам школьников Омской области, не решивших ни одного задания части «В». Причем отдельно подсчитан процент, получивших баллы за всю часть «А» и за 8 заданий части «А» (без заданий А2 и А3).
Сравним распределение первичных баллов, полученных не решившими ни одной задачи части «В» омскими школьниками, с распределением баллов, рассчитанных по формуле Бернулли. Ввиду того, что в части «А» два задания «Тождественные преобразования иррациональных выражений» — А2 и «Тождественные преобразования логарифмических выражений» — А3 решались более успешно, дополнительно вычислим результат части «А» по остальным восьми заданиям отдельно.
В результате получаем три графика, два из которых: результаты выполнения восьми заданий (без заданий А2 и А3) и результаты выполнения заданий наугад, рассчитанные по формуле Бернулли практически совпадают (рис. 3).
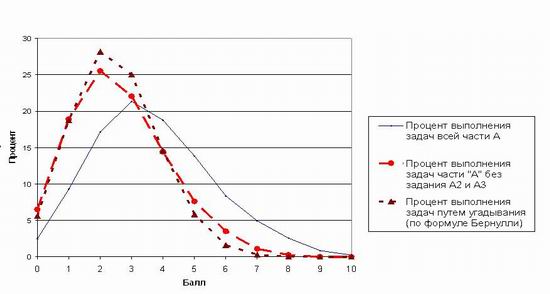
Рис.3. Выполнение заданий части «А» омскими школьниками, не решившими
часть «В»
|
Некоторое положительное смещение общих результатов части «А» у слабых учащихся объясняется относительной легкостью задач на тождественные преобразования иррациональных и логарифмических выражений, а также некоторой возможностью списать результат у сильных товарищей.
Таким образом, в 2005 году девять из одиннадцати типов задач части «А» у двоечников выполнялось с таким же успехом, как если бы ответы проставлялись наугад. К этому же выводу нас подводит также анализ решений части «А» по типам задач (см. рис.4). В целом выполнение большинства заданий с выбором ответа у школьников, получивших неудовлетворительные отметки, колеблется в пределах 20—25%, что соответствует эффективности гадания. Аналогичные результаты получает и ФИПИ [2, с.74]; [3, с. 71], [4, с. 78—79].
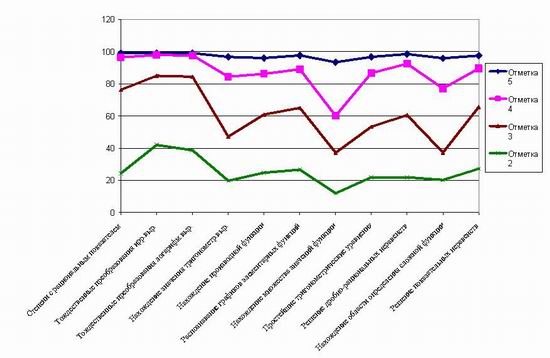
Рис. 4. Результаты выполнения части «А» омскими школьниками в процентах
|
Но если в части «А» учащиеся могли угадывать верные ответы, то в части «В» это стало невозможным. Изменение условий записи ответа немедленно отразилось на результатах. Доля верных ответов у двоечников за решение задач части «В» сразу упала до значений от 0,1% («Решение комбинированных уравнений» до 6,3% («Простейшие показательные и логарифмические уравнения»). О распространенности выполнения ЕГЭ путем подстановки ответов наугад можно судить по результативности выполнения задач на «Нахождение производной функции» (часть «А») и «Физический смысл производной» (часть «В») (т.е. близких по теме заданий). Если в части «А» с заданием «справились» (угадали) 25% получивших двойки, то в части «В» — 1,5%. Отчеты ФИПИ также фиксируют снижение результатов решения задач базового уровня сложности при переходе от части «А» к части «В» [1, с. 44]; [2, с.45], не объясняя причин. А причина проста: значительная часть школьников «участвует» на экзамене путем гадания ответов. При этом, как показал анализ, такой способ работы в экзамене более распространен среди сельских учащихся.
Нам могут возразить, что доля гадающих сильно завышена. Однако сравните успешность решения задач базового уровня сложности в части «А» и «В», например, по графикам ФИПИ [2, с.74]; [3, с.71] и вы придете к тем же выводам. Но дело даже не в этом. А в том, что ЕГЭ в принципе не может сказать, каким способом участники экзамена (кроме части «С») достигают того или иного результата, путем ли решения, гадания, подсказки, добросовестного заблуждения, логической или технической ошибки.
Факт формального отношения школьников к ЕГЭ по математике ФИПИ скрывает за такой фразой: «…в условиях экспериментального проведения ЕГЭ участнику экзамена известно заранее, что при любом выполнении работы ему обеспечена хотя бы минимальная положительная аттестационная отметка «3» по курсу алгебры и начал анализа. Очевидно, что это обстоятельство оказывает существенное влияние на отношение и, соответственно, на уровень подготовки к ЕГЭ более слабых выпускников, не предполагающих поступать в вузы, где требуется сдавать математику» [2, с.41]. Из приведенного заключения ФИПИ совершенно не ясны ни масштабы проблемы, ни инструментальные недостатки ЕГЭ. Между тем наличие на графике выброса в 27 тестовых баллов вызвано не спецификой подготовки выпускников, а формой записи результата в задачах части «А», т.е. пороками самой системы оценивания. Простые подсчеты показывают, что Единый государственный экзамен, столь «совершенный и современный» инструмент оценки качества образования, позволяет 2% участников получить удовлетворительную оценку по математике, даже не заглядывая в тексты задач. Для этого достаточно отгадать ответы 6 заданий.
В условиях невозможности определенно судить о реальных затруднениях школьников ФИПИ большое место отводит обоснованию качества контрольно-измерительных материалов. Однако у читателя нет возможности дискутировать на эту тему, поскольку действительное содержание КИМов закрыто от свободного доступа под предлогом антикоррупционной борьбы. Ссылки на возможность работать с открытым сегментом на сайте ФИПИ, где якобы находятся подлинные задачи, не должны вводить в заблуждение. На сайте вам предложат лишь потренироваться в решении нескольких вариантов или типов задач. Тем не менее, возможностей сравнить реальные варианты у вас не будет. Обсуждение проблемы при этом ФИПИ уводит в сторону оценки надежности и валидности конкретных заданий, как будто качество КИМов ограничивается только этим. Между тем совершенство экзаменационных материалов это не столько качество каждой задачи в отдельно взятом варианте работы, сколько всего комплекса заданий как единого целого, равноценность вариантов, неповторяемость заданий, альтернативы ответов и т.д. В обеспечении этих требований к КИМам нам предлагают всецело полагаться на добросовестность их создателей. И напрасно. Итоги ЕГЭ 2007 года тому свидетельство.
Спецификой 2007 года являются значительные изменения условий проведения экзамена, которые не могли не сказаться на результатах выпускников, но о которых ФИПИ умалчивает. Например, в Омской области вместо 90 вариантов работы, как это делалось в 2005—06 годах, в 2007 году школьникам было предложено лишь 15. В каждом из них существовало в среднем 3—4 задания, которые встречаются у соседей по аудитории. Опрос студентов математического факультета Омского государственного педагогического университета, сдававших ЕГЭ в 2007 году, показал, что на ЕГЭ по математике при ослаблении дисциплины был возможен обмен результатами задач, не только в части «А» и «В», но иногда даже в части «С»! Чистота проведения испытаний в такой ситуации определялась уже не столько качеством экзаменационных материалов, сколько порядком на пунктах проведения ЕГЭ.
Другим важным фактором повышения результата в 2007 году стало изменение КИМов, хотя ФИПИ уверяет, что КИМы не менялись [3, с.12]. Изменения КИМов коснулись частично характера задач (2 задачи на «Функции» были заменены на «Уравнения и неравенства» [4, с.42].), но главным образом на форму представления заданий в части «А». В заданиях КИМов 2007 года альтернативы ответов зачастую уже содержали подсказку. От школьника не требовалось знания математики, нужно было лишь немного внимания. Так, например, если в 2006 году доля омских выпускников, получивших «два» и решивших задание на производную составила 43% (сравнительно высокий для двоечников процент объясняется повторяемостью данного задания и возможностью получить подсказку), то в 2007 году — уже 60%. Это вовсе не означает, что слабые учащиеся стали лучше разбираться в материале по производной. Предлагаемые в задачах альтернативы решений позволяли найти верный ответ методом исключения, не решая задач. У учителей появился даже специальный термин для решения подобных заданий: «метод пристального всматривания». Приведем пример:
2006 год |
2007 год |
Найдите производную функции
y' = ex – 0,9x2
1) y' = xex-1 – 1,8x
2) y' = ex – 1,8x
3) y' = ex – 0,3x2
4) y' = ex – 0,81x
|
Найдите производную функции
y = 20x4 – ex
1) y' = 80x3 – xex-1
2) y' = 4x5 – ex+1 / x+1
3) y' = 80x3 – ex
4) y' = 5x3 – xex-1
|
Если в 2006 году ответ не очевиден и задачу необходимо решать, то в 2007 году верный ответ виден с первого взгляда. Конечно, хорошо, что учащиеся могут проявить такие свои качества как внимание, но для этого следует использовать тесты интеллекта. На экзамене по математике нужно проверять конкретные знания и умения. Кстати, спецификация работы 2007 года требует умения находить производную функции [3, с.77], а не угадывать ее.
Еще пример:
2006 год |
2007 год |
Найдите значение выражения log2(8a),
если log2a = –3,6
1) – 0,6 2) – 6,6 3) – 28,8 4) – 11,6
|
Найдите значение выражения 3 x 2 log25
1) log215 2) 125 3) 30 4) 15
|
В задаче 2006 года требуется сначала применить свойство логарифмов, а уж потом вычислять их. В 2007 году достаточно только знать определение логарифма. В 2006 году задание решили 26% слабых школьников (результат в области гадания), в 2007 – 43%.
Не следует думать, что авторы нарочно подобрали неудачные примеры разработчиков КИМов. Одним из главных декларируемых качеств контрольно-измерительных материалов является однотипность заданий и их одинаковая сложность. Взглянув на любой вариант работы, мы получаем достоверное представление обо всех остальных. В силу того, что омским учащимся было предложено всего лишь 15 вариантов работы, можно сделать вывод, что КИМы в 2007 году все были такими.
В своих отчетах ФИПИ совершенно умалчивает содержание предлагаемых школьникам альтернатив и ведет только обсуждение задач. Между тем, манипулируя содержанием альтернатив ответов и повторяемостью задач, ФИПИ меняет в нужную ему сторону результат экзамена. Но зачем?
Напомним, что в январе 2007 года Государственной Думой был принят Закон «О внесении изменении в Закон Российской Федерации «Об образовании» и Федеральный закон «О высшем и послевузовском профессиональном образовании» в части проведения единого государственного экзамена». Введение обязательности ЕГЭ неизбежно должно было снизить результаты, поскольку слабые школьники, которые ранее могли уклониться от сдачи экзамена, вынуждены были теперь сдавать его. Видимо для того, чтобы не портить слишком резко картину успеваемости и не вызывать критику экзамена его организаторы снизили порог требований таким способом. Однако уровень участия выпускников в 2007 году был не столь высоким, как ожидалось (в 2006 году — 47,7% и в 2007 — 52,9%). Из-за того, что регионы не торопились вводить математику в качестве обязательного испытания слабые учащиеся, как и ранее, нашли возможность уклониться от его сдачи. Результаты по стране, поэтому, оказались выше ожидаемого.
Еще одним обстоятельством, которое видимо подтолкнуло ФИПИ к манипулированию КИМами, являются итоги пробного экзамена в 2007 году. В Омской области, например, по математике был показан наихудший результат (8,69 первичных балла) за все время наблюдений (имеются в виду пробные и штатные экзамены с 2004 по 2007 год). Внесение корректив в условия проведения штатных испытаний «благотворно» отразилось на показателях успеваемости. Спустя всего два месяца, на штатном экзамене, достигнут наилучший результат по годам наблюдений (10,28 первичных балла) [7, с.13]. На рис. 2 хорошо видно как сократилась доля учащихся, находившихся ранее в зоне отметки «два» (от 0 до 38 баллов) и переместившихся в зону отметки «три» (38—54 балла). Доля хорошистов (54—72 балла) и отличников (свыше 72 баллов) при этом изменилась незначительно потому, что для получения высоких оценок необходимо было решать задания части «В» и «С». В первом случае задания не содержали альтернатив, содержащих подсказки, во втором – обмен результатами во время экзамена затруднен в силу развернутой формы ответа.
К такому росту первичного балла устроители ЕГЭ оказались явно не готовы. Поэтому без объяснения причин (ФИПИ о них ничего не сообщает) Министерство образования и науки РФ повышает норму для выставления отметки «3», т.е. именно за часть «А» и «В», где встречались повторяющиеся задачи и альтернативы ответов содержали подсказки. Шкалирование результатов 2006 и 2007 годов на основе «единого банка откалиброванных тестовых заданий» (если такое шкалирование вообще проводилось) в данном случае выполняет функцию «дымовой завесы», которая под видом математической процедуры маскирует низкое качество экзаменационных материалов и слабую дисциплину в 2007 году. Более того, именно эти, наиболее «грязные» с точки зрения чистоты проведения испытаний, результаты выставлены на сайте ФИПИ как иллюстрация состояния математической подготовки школьников (см. рис. 1). При этом ФИПИ делает вывод: «С учетом повышения нормы выставления отметки “3” можно констатировать, что наблюдается некоторая тенденция повышения уровня подготовки у части учащихся, входящих в группу слабо подготовленных выпускников» [3, с.21]. Комментарии излишни.
Еще одним пробелом работы ФИПИ является отсутствие попыток взглянуть на экзамен как социальную проблему. Если заполнение бланков наугад характеризует участие в ЕГЭ значительной части школьников, то результаты 2007 года иллюстрируют отношение к ЕГЭ со стороны учителей. В печати часто можно встретить сомнения в достоверности итогов ЕГЭ по территориям, когда лучшие показатели, например, по русскому языку демонстрируют школьники национальных республик. В связи с этим делаются выводы об особенностях менталитета и клановости населения ряда территорий, где нечестные должностные лица находят лазейки в системе безопасности экзамена и делают известными задания еще до проведения испытаний.
На самом деле, на наш взгляд, все дело в другом. Идея ЕГЭ как контроля качества педагогического труда не принята большинством учителей, в том числе и в Омской области. Фактически ЕГЭ воспринят как недоверие к учителю, его работе, справедливости и непредвзятости оценивания учебных достижений школьников. Какова в этих условиях должна быть позиция учителя, контролирующего ход проведения экзамена? – Помочь или не мешать учащимся пользоваться какой-либо помощью. Самое доступное в этом – закрыть глаза на нарушения дисциплины: подсказки, шпаргалки, сотовые телефоны и другие средства борьбы за оценку. Стоило лишь ФИПИ в 2007 году подготовить КИМы с одинаковыми заданиями, как низкая дисциплина экзамена тут же дала о себе знать ростом решения повторяющихся задач с фиксированным и кратким ответом. Ранее это явление из-за большего числа вариантов наблюдалось в существенно меньших масштабах. Однако и в 2005 году успешность «решения» слабыми учащимися задач А2 и А3 также частично объясняется повторяемостью этих заданий и возможностью обмена ответами. Важным фактором является и то обстоятельство, что все контролирующие проведение ЕГЭ инстанции и должностные лица на местах более заинтересованы в повышении результата, чем в обеспечении его объективности: это и учителя, и директора школ, и заведующие РОНО, и руководители областного (краевого) уровня.
Объективный содержательный анализ экзамена, таким образом, сталкивается с серьезными трудностями, заложенными в самой идеологии ЕГЭ (формализм результатов, ограниченность структуры данных и их несопоставимость по годам и территориям, бессмысленность анализа содержания работ на уровне всей страны), а также связанными с отношением к экзамену различных социальных групп – участников (формальное участие школьников, заинтересованность контролирующих органов в завышении оценок, низкая дисциплина проведения испытаний). На все это накладывается стремление специалистов ФИПИ минимизировать критику экзамена, что оборачивается манипуляцией КИМами, замалчиванием проблем, тенденциозностью подбора фактов и выводов по итогам ЕГЭ.
Изучение результатов ЕГЭ на региональном уровне еще более затруднено. Максимум на что могут рассчитывать региональные исследователи – это работа с протоколами экзамена, которые формируются ФЦТ. Однако в протоколах фиксируется только факт правильности ответов, без указания их содержания. Нет и информации о характере предложенных школьникам заданий. Региональная статистика экзамена сильно запутана. Авторы КИМов приложили большие усилия для обеспечения «чистоты эксперимента», заложив несоответствие расположения заданий в различных вариантах экзаменационных работ. Контрольно-измерительные материалы составляются на основе нескольких планов, являющихся модификациями общего плана, обозначенного в спецификации. За одинаковыми кодами заданий, на самом деле в вариантах скрываются задачи разных типов, не только не всегда соответствующие, но даже не указанные в спецификации (например, в 2005 году кроме задач обозначенных в спецификации в части «А» применялся такой тип как «Решение показательных неравенств»). Содержательный анализ работ учащихся в этих условиях возможен лишь при обеспечении доступа региональных исследователей к фактическим экзаменационным заданиям и действительным ответам школьников. Однако такого доступа у них нет.
Наглядным примером может служить ситуация в Омской области. Выпускаемые Министерством образования Омской области и выполняющим функции РЦОИ Региональным информационно-аналитическим центром системы образования Омской области (РИАЦ) сборники статистики по итогам ЕГЭ 2005—07 годов содержат лишь таблицы со средними тестовыми баллами муниципальных образований и образовательных учреждений, предоставляя читателям сопоставлять цифры и делать выводы самостоятельно. Среднеобластные результаты решения различных типов заданий в них приводятся по спецификации 2004(!) года. В течение трех лет омские организаторы ЕГЭ не только сами не знали, какие задачи по математике решали школьники, но вводили в заблуждение учителей области относительно их действительного характера, отсылая к недействующей уже спецификации [7, с.10—12], [8, с.50—52]. В 2008 году омский РИАЦ вообще отказался от публикации результатов решения по типам задач. Самостоятельные попытки анализа итогов ЕГЭ, выполненные РИАЦ, носят единичный и неудачный характер. Так, например, в сборнике за 2005 год РИАЦ перечисляет варианты, с которыми школьники справились лучше и хуже всего и на основании этого делает выводы об их неравнозначности. При этом даже высчитывается разница между средними величинами процентов верно выполненных «простого» и «сложного» вариантов [6, с.31]. Однако составители сборника не обратили внимания на контингент учащихся эти варианты решавших. Так называемые «простые» варианты были распространенны среди более подготовленных городских школьников, а «сложные» — среди сравнительно слабых сельских.
В то же время именно на региональном уровне и уровне муниципалитетов содержательный разбор итогов был бы наиболее продуктивен. Результаты экзамена было бы неплохо сопоставлять с показателями ведомственной статистики (образовательный, квалификационный и возрастной состав учителей, распределение нагрузки, наполняемость классов, режим работы образовательных учреждений, система подвоза учащихся из отдаленных сел, характер контингента школьников и другие местные особенности).
Однако в действующей системе распределения информации, какие бы формы и направление не принял анализ региональных итогов, он с неизбежностью содержит в себе ошибки и погрешности, заложенные формой организации ЕГЭ:
1) невозможно подвести итоги работ учащихся, не зная, какие задачи они решают;
2) подведение итогов по кодам задач и сделанные в условиях отсутствия доступа к их содержанию выводы, ориентирует педагогов на типы заданий, которые школьникам иногда даже не предлагались;
3) без анализа конкретных ответов невозможно судить о характере ошибок и затруднений учащихся;
4) сравнение усредненных баллов образовательных учреждений региона базируется на допущении, что экзамен повсеместно проводится в одинаково стерильных условиях, что далеко не так;
5) в регионах отсутствует алгоритм анализа результатов ЕГЭ, а работы ФИПИ из-за различий в уровне доступности к исходной информации не могут служить на местах стандартом исследования.
Одним из аргументов введения ЕГЭ часто называют контроль качества образования и возможность образовательных учреждений, органов управления проанализировать результативность школ по подготовке учащихся. Конкретная практика проведения ЕГЭ свидетельствует об обратном. ЕГЭ, в нынешнем его виде, не оправдывает ожиданий ни как инструмент анализа уровня математической подготовки учащихся и ни тем более как инструмент повышения качества образования. Об этом говорят уже сами организаторы экзамена: «Единый государственный экзамен призван выявить уровень и качество общеобразовательной подготовки выпускников, но не может изменить состояние образования в стране» [3, с.20].
Совершенно очевидно, что первым шагом для повышения качества подготовки школьников является доведение до учителей школ и муниципальных органов управления образованием информации об итогах экзамена в полном объеме. Каждый учитель должен знать, какие конкретно задания решали его ученики, и какие ошибки они при этом сделали. Лучшим выходом был бы постоянно открытый банк заданий, из которого варианты ЕГЭ с учетом требований равноценности и неповторяемости ежегодно формируются случайным образом. За составителями экзаменационных заданий, таким образом, был бы установлен определенный общественный контроль, судя по 2007 году весьма полезный для всех участников ЕГЭ.
Сопоставление результатов должно осуществляться заинтересованными лицами и организациями в пределах своей компетенции. На уровне класса и школы нужно сравнивать учащихся, на уровне муниципалитетов – школы, на уровне субъекта Федерации – муниципалитеты. На уровне федерального центра итоги ЕГЭ необходимо подводить в той мере, в какой это необходимо для определения содержания образования и контрольно-измерительных материалов.
Следует устранить или нивелировать инструментальные погрешности ЕГЭ – минимизировать возможность угадывания ответов путем увеличения числа заданий отрытого типа. В заданиях с выбором ответа необходимо увеличить число альтернатив.
Необходимо отказаться от крайностей ЕГЭ и фанатизма в его применении. Во-первых, информационно-аналитическая ценность результатов ЕГЭ в сравнении с масштабами затрат ничтожна. Во-вторых, не все предметы можно втиснуть в прокрустово ложе тестов (например, литература). В-третьих, ЕГЭ не оправдывает ожиданий в точности оценки достижений учащихся. Один только его результат не является обоснованным критерием подготовки абитуриентов по причине неустранимых дефектов инструмента оценивания (тесты), в силу существенных различий характера и формы предлагаемых заданий (что особенно проявляется при сравнении итогов разных лет), дисциплины на пунктах приема экзамена и уровня «натасканности» выпускников на решение заданий в виде тестов. Поэтому в вузах необходимо вводить устный экзамен по профилирующим предметам.
Очевидно, следует также организационно развести структуры, осуществляющие разработку контрольно-измерительных материалов и анализирующие итоги испытаний. В противном случае трудно рассчитывать на объективное и беспристрастное рассмотрение проблем и результатов ЕГЭ в будущем. Для региональных органов управления образованием необходимо также разработать алгоритмы анализа и сопоставления данных, получаемых на экзамене.
Подведем итоги.
Система информации о результатах ЕГЭ оказалась поставленной «с ног на голову»: те, кто обладает исходными данными (ФИПИ), проанализировать их не могут. Те, кому информация необходима в первую очередь, прежде всего учителя, ее почти лишены. Аттестационные отметки и тестовые баллы, которые в лучшем случае доводятся до учителей, ничего не сообщают о реальных проблемах школьников.
Отсутствие сведений о характере затруднений выпускников ведет к тому, что педагоги зачастую дезориентированы в направлениях подготовки. Не случайно ФИПИ из года в год сетует на повторяющиеся типичные ошибки на экзаменах [1, с.16], [2, с.77], [3, с.50], а уровень математической подготовки школьников почти не меняется [3, с.46].
Закрытость информации и отсутствие общественного контроля за содержанием экзаменационных работ создает возможность манипуляции результатами ЕГЭ, что уже не имеет никакого отношения к главной его цели – объективной оценке уровня математической подготовки школьников. Режим излишней секретности более обслуживает корпоративные интересы организаторов ЕГЭ и покрывает огрехи их работы, чем служит повышению качества обучения математике.
Как инструмент оценки знаний ЕГЭ обладает изъянами, которые существенным образом сказываются на его результатах.
Объективность и точность результатов ЕГЭ весьма относительны, порочность натаскивания школьников на решение тестов — общепризнанна.
Библиографический список
Результаты Единого государственного экзамена (май—июнь 2005 года) Аналитический отчет, ФИПИ, Москва, 2005
Результаты Единого государственного экзамена (май—июнь 2006 года) Аналитический отчет, ФИПИ, Москва, 2006
Результаты Единого государственного экзамена, 2007 год, Аналитический отчет, ФИПИ, (http://fipi.ru/view/sections/138/docs/318.html)
Результаты Единого государственного экзамена (май—июнь 2008 года), ФИПИ, Москва, 2008, (http://fipi.ru/view/sections/138/docs/401.html)
Образование в Российской Федерации: 2006. Статистический ежегодник, М., ГУ-ВШЭ, 2006.
Статистика основных результатов Единого государственного экзамена в Омской области в мае – июне 2005г., Омск, 2005.
Статистика результатов пробного Единого государственного экзамена 12 апреля 2007г., Омск, РИАЦ, 2007
Статистика результатов Единого государственного экзамена в 2007 году в Омской области, Омск, 2007.
Примечания
По этой теме читайте также:




